θ = 0°
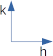
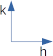
First we will look at the Ewald sphere in 3D, and how it tells us about the diffraction pattern.
In the centre panel, you can see a diffraction experiment with an X-ray beam hitting a crystal from the left. On the right is a detector, which is initially blank. The Ewald sphere is shown in red, with the reciprocal lattice centred on its surface. Remember that the Ewald sphere and the reciprocal lattice are not real, they are mathematical constructions which tell us when the conditions for diffraction are met - whenever a reciprocal lattice spot crosses the Ewald sphere.
In the left panel are the controls. The buttons at the top rotate the crystal (and the reciprocal lattice rotates with it). When it is rotated far enough for a spot to cross the Ewald sphere, this will be highlighted on the sphere with a blue dot, a line will be drawn following the diffracted beam from the crystal to the detector, and a spot will appear on the detector. Use the ↶ button to rotate the crystal to θ = 8°, and you should see the (010) spot appear. (h is to the right, k is up, and l is out of the screen.) Use the slider at the bottom of the controls to look at the scene from different angles.
Continue rotate the crystal to θ = 15°, at which point 3 more spots will appear: (011), (011), and (020). At what angle do the (021) and (021) spots appear? If you continue to rotate the crystal to θ = 30° some spots appear on the bottom half of the detector. These have a different h value. Can you deduce their indices?