Cubic unit cell powder diffraction

In the case of diffraction from a powder, we have a huge number of micro crystals in random orientations, which means that every possible diffraction spot will appear at once. This also means that each spot will be smeared out into ring because different micro crystals will be in different orientations around the beam axis.

The applet still shows a single (micro) crystal that you can rotate to see spots cross the Ewald sphere, however the diffraction pattern now shows the powder diffraction rings. In reality these would all appear at once without rotating the crystal.

For a cubic crystal, the rings form an easily recognized pattern, corresponding to diffraction vectors whose lengths are in the ratios 1 : √2 : √3 : 2 : √5 : √6 : √8 : 3, based on the possible values of hkl in the following equation:

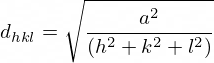
The rings can be indexed by the hkl of the corresponding spots, i.e. (100), (110), (111), (200), (210), (211), (220), (300) and their permutations respectively. In some cases some of these rings can be missing due to the symmetries of the unit cell.